Python tiene listas, enteros, punto flotante, etc. Para cálculo numérico necesitamos más... allí aparece Numpy.
Numpy es un paquete que provee a Python con arreglos multidimensionales de alta eficiencia y diseñados para cálculo científico.
Un array puede contener:
- tiempos discretos de un experimento o simulación.
- señales grabadas por un instrumento de medida.
- pixeles de una imagen, etc.

In [1]:

%matplotlib inline

In [2]:

import numpy as np

3.2. El objeto arreglo.¶

Los arreglos de NumPy son de tipado estático y homogéneo.
Son más eficientes en el uso de la memoria.
La funciones matemáticas complejas y computacionalmente costosas (pj: la multiplicación de matrices) son implementadas en lenguajes compilados como C o Fortran.

3.2.1. Creación de arreglos unidimensionales.¶

A partir de una lista de Python:

In [3]:

lista = [1, 2, 3, 4 , 5]

In [4]:

type(lista)

Out[4]:

list

In [5]:

a = np.array(lista)

In [6]:

Out[6]:

array([1, 2, 3, 4, 5])

In [7]:

type(a)

Out[7]:

numpy.ndarray

Podemos conocer el tipo de datos a través de dtype:

In [8]:

a.dtype

Out[8]:

dtype('int64')

Incluso podemos definir el tipo de dato al momento de la creación de arreglo:

In [9]:

a_complejo = np.array(lista, dtype=complex)

In [10]:

a_complejo

Out[10]:

array([ 1.+0.j,  2.+0.j,  3.+0.j,  4.+0.j,  5.+0.j])

In [11]:

a_complejo.dtype

Out[11]:

dtype('complex128')

o cambiar el tipo de dato:

In [12]:

a_no_mas_complejo = a_complejo.astype(np.int64)

-c:1: ComplexWarning: Casting complex values to real discards the imaginary part

In [13]:

a_no_mas_complejo

Out[13]:

array([1, 2, 3, 4, 5])

Si queremos ver algunas características del arreglo a:

In [14]:

a.ndim # dimensión

Out[14]:

In [15]:

a.shape # 5 x 1

Out[15]:

(5,)

In [16]:

len(a) # elementos en la primera dimension

Out[16]:

3.2.2. Creación de arreglos de 2 y 3 dimensiones.¶

In [17]:

b = np.array([[0, 1, 2], [3, 4, 5]]) # arreglo 2 x 3

In [18]:

Out[18]:

array([[0, 1, 2],
       [3, 4, 5]])

In [19]:

b.ndim

Out[19]:

In [20]:

b.shape

Out[20]:

(2, 3)

In [21]:

len(b) # elementos en la primera dimensión

Out[21]:

In [22]:

c = np.array([[[1], [2]], [[3], [4]]])

In [23]:

Out[23]:

array([[[1],
        [2]],

       [[3],
        [4]]])

In [24]:

c.shape

Out[24]:

(2, 2, 1)

In [25]:

a = np.arange(10) # otra forma de generar un arreglo: a través de funciones específicas de numpy

In [26]:

Out[26]:

array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])

In [27]:

a[0], a[2], a[-1]

Out[27]:

(0, 2, 9)

In [28]:

mis_indices = [0, 2, -1] # puedo listar índices

In [29]:

a[mis_indices] # y luego indexar por esa lista ("fancy indexing")

Out[29]:

array([0, 2, 9])

In [30]:

Out[30]:

array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])

In [31]:

a[2:9] # corta en intervalos

Out[31]:

array([2, 3, 4, 5, 6, 7, 8])

In [32]:

a[2:9:3] # puedo especificar cada cuánto cortar

Out[32]:

array([2, 5, 8])

In [33]:

a[::2]

Out[33]:

array([0, 2, 4, 6, 8])

In [34]:

a[3::2]

Out[34]:

array([3, 5, 7, 9])

In [35]:

a[-2:]

Out[35]:

array([8, 9])

Un esquema siempre ayuda...

3.2.5. Copias y Vistas.¶

Si copiamos una lista en Python... si modificamos la copia, no se modifica la lista originalmente copiada:

In [36]:

%%python
# python cell magic, lindo... no?
a = [1, 2, 3]
b = a[:]
print b
b[0] = 100
print b
print a

[1, 2, 3]
[100, 2, 3]
[1, 2, 3]

Si trabajamos con arreglos de NumPy, el comportamiento es diferente (cuando copiamos, en realidad, estamos haciendo una vista al objeto original, apuntamos al mismo objeto):

In [37]:

a = np.array([1, 2, 3])
b = a[:]
print b
b[0] = 100
print b
print a

[1 2 3]
[100   2   3]
[100   2   3]

¿Cómo resolvemos esta discrepancia?

In [38]:

a = np.array([1, 2, 3])
b = a[:].copy() # fuerzo la copia
print b
b[0] = 100
print b
print a

[1 2 3]
[100   2   3]
[1 2 3]

3.3. Operaciones numéricas sobre arreglos.¶

3.3.1. Operaciones por elementos.¶

In [39]:

a = np.array([1, 2, 3, 4])

In [40]:

a + 1

Out[40]:

array([2, 3, 4, 5])

In [41]:

2**a

Out[41]:

array([ 2,  4,  8, 16])

In [42]:

b = np.ones(4) # otra función generadora de arreglos
b = b + 1
b

Out[42]:

array([ 2.,  2.,  2.,  2.])

In [43]:

b - a

Out[43]:

array([ 1.,  0., -1., -2.])

In [44]:

a * b

Out[44]:

array([ 2.,  4.,  6.,  8.])

In [45]:

c = np.ones((3, 3))
c

Out[45]:

array([[ 1.,  1.,  1.],
       [ 1.,  1.,  1.],
       [ 1.,  1.,  1.]])

In [46]:

c * c # ojo! esto es una multiplicación elemento por elemento.

Out[46]:

array([[ 1.,  1.,  1.],
       [ 1.,  1.,  1.],
       [ 1.,  1.,  1.]])

In [47]:

c.dot(c) # multiplicación matricial

Out[47]:

array([[ 3.,  3.,  3.],
       [ 3.,  3.,  3.],
       [ 3.,  3.,  3.]])

In [48]:

a = np.array([1, 2, 3, 4])
b = np.array([4, 2, 2, 4])

In [49]:

a == b

Out[49]:

array([False,  True, False,  True], dtype=bool)

In [50]:

a > b

Out[50]:

array([False, False,  True, False], dtype=bool)

Otras operaciones lógicas:

In [51]:

a = np.array([1, 1, 0, 0], dtype=bool)
b = np.array([1, 0, 1, 0], dtype=bool)

In [52]:

a | b # or, np.logical_or

Out[52]:

array([ True,  True,  True, False], dtype=bool)

In [53]:

a & b # and, np.logical_and

Out[53]:

array([ True, False, False, False], dtype=bool)

In [54]:

a ^ b # xor, np.logical_xor

Out[54]:

array([False,  True,  True, False], dtype=bool)

In [55]:

not_a = - a # not, np.logical_not
not_a

Out[55]:

array([False, False,  True,  True], dtype=bool)

3.3.2. Reducciones básicas.¶

In [56]:

x = np.array([1, 2, 3, 4])

In [57]:

x.sum() # np.sum(x)

Out[57]:

por filas y columnas:

In [58]:

x = np.array([[1, 1], [2, 2]])

In [59]:

x.sum(axis=0) # por columna

Out[59]:

array([3, 3])

In [60]:

x[:,0].sum(), x[:,1].sum()

Out[60]:

(3, 3)

In [61]:

x.sum(axis=1) # por filas

Out[61]:

array([2, 4])

In [62]:

x[0,:].sum(), x[1,:].sum()

Out[62]:

(2, 4)

Calculando estadísticos:

In [63]:

x = np.array([1, 2, 3, 1])

In [64]:

x.mean()

Out[64]:

1.75

In [65]:

x.std()

Out[65]:

0.82915619758884995

In [66]:

x.std(ddof=1) # con divisor n - 1

Out[66]:

0.9574271077563381

In [67]:

np.median(x)

Out[67]:

1.5

In [68]:

y = np.array([[1, 2, 3], [5, 6, 1]])

In [69]:

np.median(y, axis=-1) # último eje: en este caso, filas

Out[69]:

array([ 2.,  5.])

Encontrando extremos:

In [70]:

x.min()

Out[70]:

In [71]:

np.argmin(x) # índice del mínimo

Out[71]:

In [72]:

x.max()

Out[72]:

In [73]:

np.argmax(x) # índice del máximo

Out[73]:

Más operaciones lógicas:

In [74]:

np.all([True, True, False])

Out[74]:

False

In [75]:

np.any([True, True, False])

Out[75]:

True

3.3.3. Broadcasting.¶

En NumPy es posible hacer operaciones entre arreglos de diferente tamaño a través del broadcasting.

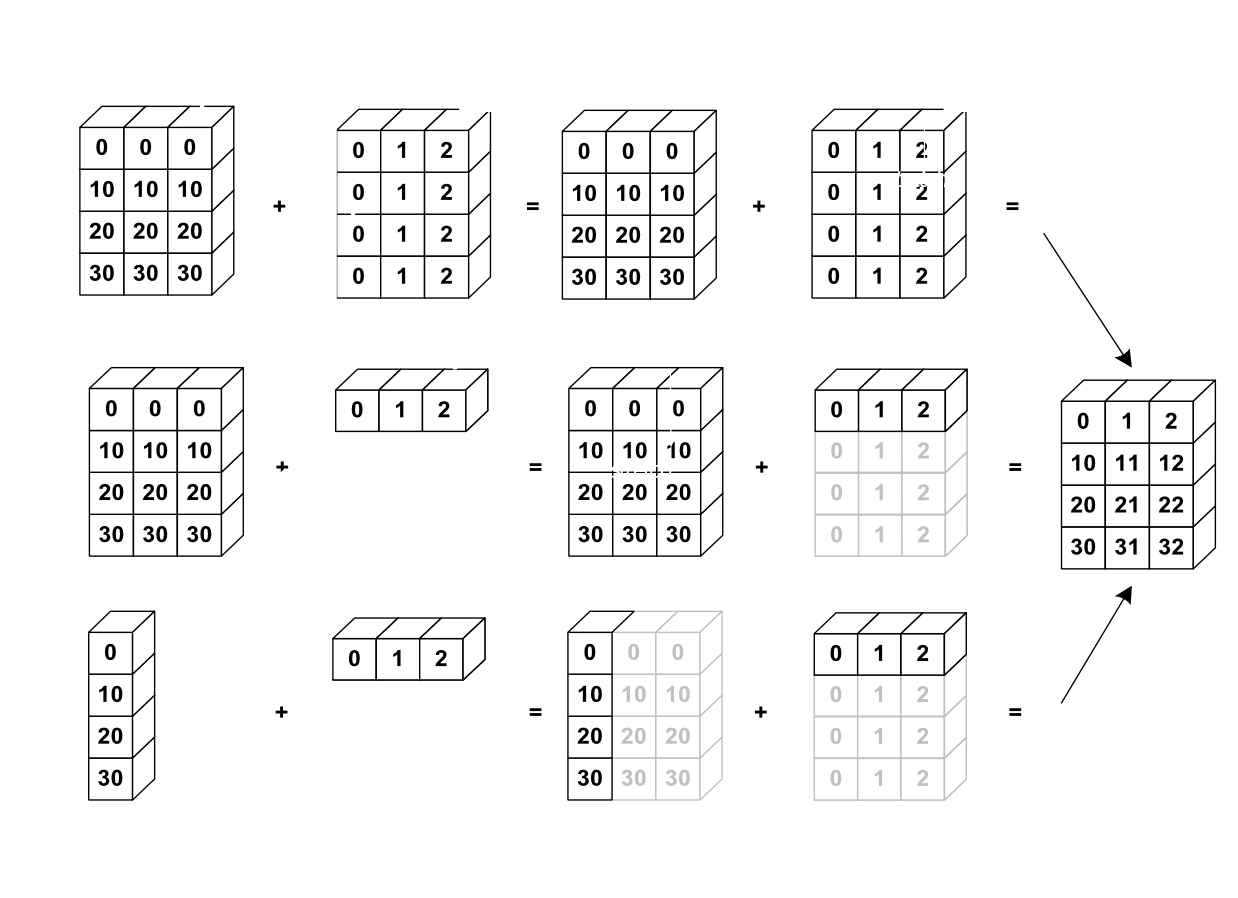
NumPy transforma (propaga) los arreglos involucrados para que tengan el mismo tamaño y, por tanto, puedan someterse a las operaciones por elementos sin generar excepciones.

In [76]:

a = np.arange(0, 40, 10)
a.shape

Out[76]:

(4,)

In [77]:

a = a[:, np.newaxis]  # suma un nuevo eje (arreglo 2D)
a.shape
a

Out[77]:

array([[ 0],
       [10],
       [20],
       [30]])

In [78]:

b = np.array([0, 1, 2])
b

Out[78]:

array([0, 1, 2])

In [79]:

a + b

Out[79]:

array([[ 0,  1,  2],
       [10, 11, 12],
       [20, 21, 22],
       [30, 31, 32]])

3.3.4. Álgebra lineal básica.¶

Multiplicaión de matrices:

In [80]:

a = np.triu(np.ones((3, 3)), 1)   # see help(np.triu)
a

Out[80]:

array([[ 0.,  1.,  1.],
       [ 0.,  0.,  1.],
       [ 0.,  0.,  0.]])

In [81]:

b = np.diag([1, 2, 3])
b

Out[81]:

array([[1, 0, 0],
       [0, 2, 0],
       [0, 0, 3]])

In [82]:

a.dot(b)

Out[82]:

array([[ 0.,  2.,  3.],
       [ 0.,  0.,  3.],
       [ 0.,  0.,  0.]])

In [83]:

a.T

Out[83]:

array([[ 0.,  0.,  0.],
       [ 1.,  0.,  0.],
       [ 1.,  1.,  0.]])

Inversión y resolución de equaciones lineales:

In [84]:

A = a + b
A

Out[84]:

array([[ 1.,  1.,  1.],
       [ 0.,  2.,  1.],
       [ 0.,  0.,  3.]])

In [85]:

B = np.linalg.inv(A)
B

Out[85]:

array([[ 1.        , -0.5       , -0.16666667],
       [ 0.        ,  0.5       , -0.16666667],
       [ 0.        ,  0.        ,  0.33333333]])

In [86]:

B.dot(A)

Out[86]:

array([[ 1.,  0.,  0.],
       [ 0.,  1.,  0.],
       [ 0.,  0.,  1.]])

In [87]:

x = np.linalg.solve(A, [1, 2, 3])
x

Out[87]:

array([-0.5,  0.5,  1. ])

In [88]:

A.dot(x)

Out[88]:

array([ 1.,  2.,  3.])

Cálculo de autovalores:

In [89]:

np.linalg.eigvals(A)

Out[89]:

array([ 1.,  2.,  3.])

3.4. Manipulación de arreglos.¶

3.4.1. Manipulación de la forma de los arreglos.¶

In [90]:

a = np.array([[1, 2, 3], [4, 5, 6]])

In [91]:

a.ravel()

Out[91]:

array([1, 2, 3, 4, 5, 6])

In [92]:

a.T

Out[92]:

array([[1, 4],
       [2, 5],
       [3, 6]])

In [93]:

a.T.ravel()

Out[93]:

array([1, 4, 2, 5, 3, 6])

In [94]:

a.shape

Out[94]:

(2, 3)

In [95]:

b = a.ravel()
b

Out[95]:

array([1, 2, 3, 4, 5, 6])

In [96]:

b.reshape((2,3))

Out[96]:

array([[1, 2, 3],
       [4, 5, 6]])

In [97]:

a = np.arange(36)

In [98]:

b = a.reshape((6,6))
b

Out[98]:

array([[ 0,  1,  2,  3,  4,  5],
       [ 6,  7,  8,  9, 10, 11],
       [12, 13, 14, 15, 16, 17],
       [18, 19, 20, 21, 22, 23],
       [24, 25, 26, 27, 28, 29],
       [30, 31, 32, 33, 34, 35]])

In [99]:

b = a.reshape((6, -1)) # -1: comodín, se infiere
b

Out[99]:

array([[ 0,  1,  2,  3,  4,  5],
       [ 6,  7,  8,  9, 10, 11],
       [12, 13, 14, 15, 16, 17],
       [18, 19, 20, 21, 22, 23],
       [24, 25, 26, 27, 28, 29],
       [30, 31, 32, 33, 34, 35]])

In [100]:

a = np.arange(4)
a.resize((8,))
a

Out[100]:

array([0, 1, 2, 3, 0, 0, 0, 0])

Agregado de nuevas dimensiones:

In [101]:

vector = np.array([1,2,3])
vector

Out[101]:

array([1, 2, 3])

In [102]:

np.shape(vector)

Out[102]:

(3,)

In [103]:

matrix_col = vector[:, np.newaxis] # lo convierto en matrix 3 x 1
matrix_col

Out[103]:

array([[1],
       [2],
       [3]])

In [104]:

np.shape(matrix_col)

Out[104]:

(3, 1)

In [105]:

matrix_ver = vector[np.newaxis, :] # lo convierto en matrix 1 x 3
matrix_ver

Out[105]:

array([[1, 2, 3]])

In [106]:

np.shape(matrix_ver)

Out[106]:

(1, 3)

In [107]:

a = np.array([[1, 2], [3, 4]])
a

Out[107]:

array([[1, 2],
       [3, 4]])

In [108]:

np.repeat(a, 3)

Out[108]:

array([1, 1, 1, 2, 2, 2, 3, 3, 3, 4, 4, 4])

In [109]:

np.tile(a, 3)

Out[109]:

array([[1, 2, 1, 2, 1, 2],
       [3, 4, 3, 4, 3, 4]])

In [110]:

b = np.array([[5, 6]])

In [111]:

np.concatenate((a, b), axis=0)

Out[111]:

array([[1, 2],
       [3, 4],
       [5, 6]])

In [112]:

np.concatenate((a, b.T), axis=1)

Out[112]:

array([[1, 2, 5],
       [3, 4, 6]])

In [113]:

np.vstack((a,b))

Out[113]:

array([[1, 2],
       [3, 4],
       [5, 6]])

In [114]:

np.hstack((a,b.T))

Out[114]:

array([[1, 2, 5],
       [3, 4, 6]])

3.4.2. Funciones para tomar datos de los arreglos.¶

In [115]:

a = np.array([1,0,1,0,0], dtype=bool)
b = np.where(a) # where
b

Out[115]:

(array([0, 2]),)

In [116]:

a = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
a

Out[116]:

array([[1, 2, 3],
       [4, 5, 6],
       [7, 8, 9]])

In [117]:

np.diag(a) # diag

Out[117]:

array([1, 5, 9])

In [118]:

a = np.arange(10,16)
a

Out[118]:

array([10, 11, 12, 13, 14, 15])

In [119]:

indices = [1, 3, 5]

In [120]:

np.take(a, indices)

Out[120]:

array([11, 13, 15])

In [121]:

which = [0, 0, 1, 0]
choices = [[-2, -3, -4, -5], [5, 6, 7, 8]]
np.choose(which, choices)

Out[121]:

array([-2, -3,  7, -5])

3.4.3. Funciones generadoras de arreglos.¶

In [122]:

x = np.arange(0, 10, 1) # argumentos: inicio, fin, paso
x

Out[122]:

array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])

In [123]:

np.linspace(0, 10, 25) # incio, fin, n° puntos intermedios

Out[123]:

array([  0.        ,   0.41666667,   0.83333333,   1.25      ,
         1.66666667,   2.08333333,   2.5       ,   2.91666667,
         3.33333333,   3.75      ,   4.16666667,   4.58333333,
         5.        ,   5.41666667,   5.83333333,   6.25      ,
         6.66666667,   7.08333333,   7.5       ,   7.91666667,
         8.33333333,   8.75      ,   9.16666667,   9.58333333,  10.        ])

In [124]:

np.logspace(0, 10, 10, base=np.e)

Out[124]:

array([  1.00000000e+00,   3.03773178e+00,   9.22781435e+00,
         2.80316249e+01,   8.51525577e+01,   2.58670631e+02,
         7.85771994e+02,   2.38696456e+03,   7.25095809e+03,
         2.20264658e+04])

In [125]:

x, y = np.mgrid[0:5, 0:5] # similar al meshgrid de MATLAB

In [126]:

Out[126]:

array([[0, 0, 0, 0, 0],
       [1, 1, 1, 1, 1],
       [2, 2, 2, 2, 2],
       [3, 3, 3, 3, 3],
       [4, 4, 4, 4, 4]])

In [127]:

Out[127]:

array([[0, 1, 2, 3, 4],
       [0, 1, 2, 3, 4],
       [0, 1, 2, 3, 4],
       [0, 1, 2, 3, 4],
       [0, 1, 2, 3, 4]])

In [128]:

np.random.rand(5, 5) # números aleatorios uniformes [0,1]

Out[128]:

array([[ 0.71993812,  0.05176951,  0.37876399,  0.71104661,  0.09103074],
       [ 0.66332802,  0.56448753,  0.6795584 ,  0.19281203,  0.62263155],
       [ 0.96436095,  0.06478416,  0.05179043,  0.391897  ,  0.96105272],
       [ 0.05728427,  0.55147176,  0.3245483 ,  0.25468026,  0.66221203],
       [ 0.55938751,  0.5883277 ,  0.9253775 ,  0.27429514,  0.3440919 ]])

In [129]:

np.random.randn(5,5) # números aleatorios normalmente distribuidos

Out[129]:

array([[-0.65733   , -0.39731405,  1.7341414 ,  0.3567832 ,  1.69461793],
       [ 1.54425562, -1.82893025, -0.15648911,  0.66672057,  0.66853341],
       [ 0.83117805,  1.17071038, -0.81596502,  0.5750493 , -0.63990098],
       [-0.56259403,  0.45052975, -0.43402709, -0.40855709, -0.70216341],
       [-0.58823829, -1.05708393,  1.21155867,  0.84643448,  2.0027709 ]])

In [130]:

np.diag([1,2,3]) # matrix diagonal

Out[130]:

array([[1, 0, 0],
       [0, 2, 0],
       [0, 0, 3]])

In [131]:

np.diag([1,2,3], k=1) # desplazamiento sobre la diagonal

Out[131]:

array([[0, 1, 0, 0],
       [0, 0, 2, 0],
       [0, 0, 0, 3],
       [0, 0, 0, 0]])

In [132]:

np.zeros((3,3))

Out[132]:

array([[ 0.,  0.,  0.],
       [ 0.,  0.,  0.],
       [ 0.,  0.,  0.]])

In [133]:

np.ones((3,3))

Out[133]:

array([[ 1.,  1.,  1.],
       [ 1.,  1.,  1.],
       [ 1.,  1.,  1.]])

3.4.4. Entrada/Salida¶

Podemos leer archivos csv:

In [134]:

!head stockholm_td_adj.dat

1800  1  1    -6.1    -6.1    -6.1 1
1800  1  2   -15.4   -15.4   -15.4 1
1800  1  3   -15.0   -15.0   -15.0 1
1800  1  4   -19.3   -19.3   -19.3 1
1800  1  5   -16.8   -16.8   -16.8 1
1800  1  6   -11.4   -11.4   -11.4 1
1800  1  7    -7.6    -7.6    -7.6 1
1800  1  8    -7.1    -7.1    -7.1 1
1800  1  9   -10.1   -10.1   -10.1 1
1800  1 10    -9.5    -9.5    -9.5 1

In [135]:

data = np.genfromtxt('stockholm_td_adj.dat')
data.shape

Out[135]:

(77431, 7)

In [136]:

data

Out[136]:

array([[  1.80000000e+03,   1.00000000e+00,   1.00000000e+00, ...,
         -6.10000000e+00,  -6.10000000e+00,   1.00000000e+00],
       [  1.80000000e+03,   1.00000000e+00,   2.00000000e+00, ...,
         -1.54000000e+01,  -1.54000000e+01,   1.00000000e+00],
       [  1.80000000e+03,   1.00000000e+00,   3.00000000e+00, ...,
         -1.50000000e+01,  -1.50000000e+01,   1.00000000e+00],
       ..., 
       [  2.01100000e+03,   1.20000000e+01,   2.90000000e+01, ...,
          4.20000000e+00,   4.20000000e+00,   1.00000000e+00],
       [  2.01100000e+03,   1.20000000e+01,   3.00000000e+01, ...,
         -1.00000000e-01,  -1.00000000e-01,   1.00000000e+00],
       [  2.01100000e+03,   1.20000000e+01,   3.10000000e+01, ...,
         -3.30000000e+00,  -3.30000000e+00,   1.00000000e+00]])

pero también podemos escribirlos:

In [137]:

M = np.random.rand(3,3)
M

Out[137]:

array([[ 0.12192489,  0.5600679 ,  0.98467243],
       [ 0.91231303,  0.75122357,  0.54310547],
       [ 0.18771526,  0.33981397,  0.48772906]])

In [138]:

np.savetxt("random-matrix.csv", M)

In [139]:

!cat random-matrix.csv

1.219248903542134999e-01 5.600678957725345741e-01 9.846724267415249976e-01
9.123130259426238675e-01 7.512235706886890574e-01 5.431054672782125170e-01
1.877152580076981714e-01 3.398139715902742664e-01 4.877290607674301670e-01

In [140]:

np.savetxt("random-matrix.csv", M, fmt='%.5f') # fmt especifica el formato a escribir

In [141]:

!cat random-matrix.csv

0.12192 0.56007 0.98467
0.91231 0.75122 0.54311
0.18772 0.33981 0.48773

In [142]:

np.save("random-matrix.npy", M)
!file random-matrix.npy

random-matrix.npy: data

In [143]:

np.load("random-matrix.npy")

Out[143]:

array([[ 0.12192489,  0.5600679 ,  0.98467243],
       [ 0.91231303,  0.75122357,  0.54310547],
       [ 0.18771526,  0.33981397,  0.48772906]])

3. Numpy.¶

3.1. Descripción.¶